1.插入排序算法的基本思想
每步将一个待排序的对象,按其排序码大小,插入到前面已经排好序的一组对象的适当位置上,直到对象全部插入为止。
2.插入排序算法的分类
根据寻找插入位置方法分为:
(1)直接插入排序
(2)折半(二分)插入排序
(3)希尔插入排序
(4)直接插入排序
3.插入排序算法的具体过程
当插入第i(i≥1)个对象时,前面的V[0],V[1],…,V[i−1]已经排好序。这时,用V[i]的排序码与V[i−1],V[i−2],…,V[0]的排序码顺序进行比较,找到插入位置即将V[i]插入,原来位置上的对象向后顺移。
直接插入排序示意图:
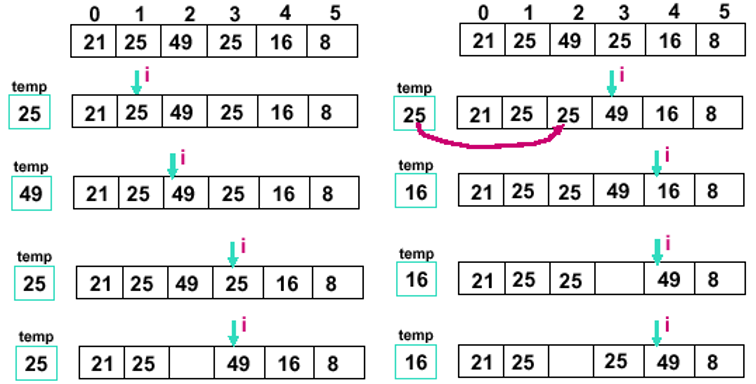
直接插入排序
从上到下,分别展示了直接排序算法的所有可能的过程,包括相同排序码的排序方式(保持了原来的顺序,说明是稳定排序)以及in-place操作中的元素移动等。
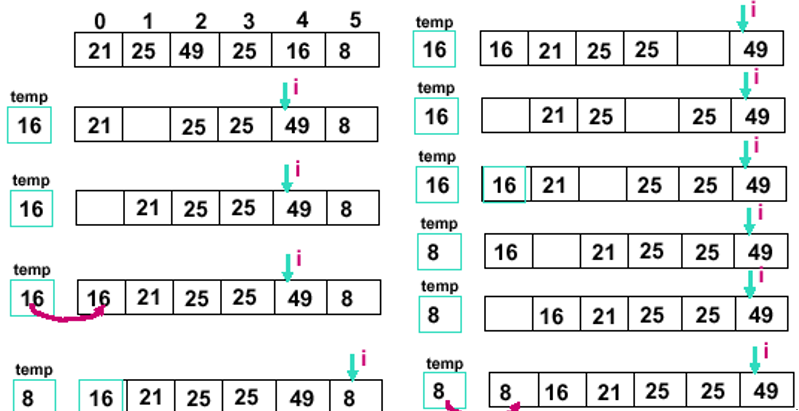
直接插入排序
4.直接插入排序算法分析
设待排序对象个数为n,则该算法的主程序执行n−1趟排序码比较次数和对象移动次数与对象排序码的初始排列有关。
最好情况下,排序前对象已经按照要求的有序。比较次数(KCN):n−1 ; 移动次数(RMN):为0。则对应的时间复杂度为O(n)。
最坏情况下,排序前对象为要求的顺序的反序。第i趟时第i个对象必须与前面i个对象都做排序码比较,并且每做1次比较就要做1次数据移动(具体可以从下面给出的代码中看出)。比较次数(KCN):∑n−1i=1i=n(n−1)2≈n22 ; 移动次数(RMN):为∑n−1i=1i=n(n−1)2≈n22。则对应的时间复杂度为O(n2)。
如果排序记录是随机的,那么根据概率相同的原则,在平均情况下的排序码比较次数和对象移动次数约为n24,因此,直接插入排序的时间复杂度为O(n2)。
5.直接插入排序算法的特点
(1)它是稳定排序,不改变相同元素原来的顺序。
(2)它是in-place排序,只需要O(1)的额外内存空间。
(3)它是在线排序,可以边接收数据边排序。
(4)它跟我们牌扑克牌的方式相似。
(5)对小数据集是有效的。
6.插入排序C语言源代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 | /** * 算法君:一个专业的算法学习分享网站 * 算法君:专业分享--数据剖析--算法精解 * 算法君:http://www.suanfajun.com */ #include<stdio.h> //插值查找-C语言实现 //基本思路:二分查找改进版,只需改一行代码。 // mid=low+(key-a[low])/(a[high]-a[low])*(high-low) int insertSearch(int *sortedSeq, int seqLength, int keyData); int main() { int array[] = { 1, 2, 3, 4, 5, 6, 7, 8, 9 }; int location; int target = 4; location = insertSearch(array, 9, target); printf("%d\n", location); return 0; } int insertSearch(int *sortedSeq, int seqLength, int keyData) { int low = 0, mid, high = seqLength - 1; while (low <= high) { mid = low + (keyData - sortedSeq[low]) / (sortedSeq[high] - sortedSeq[low]); if (keyData < sortedSeq[mid]) { high = mid - 1;//是mid-1,因为mid已经比较过了 } else if (keyData > sortedSeq[mid]) { low = mid + 1; } else { return mid; } } return -1; } |
7.插入排序C++源代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 | /** * 算法君:一个专业的算法学习分享网站 * 算法君:专业分享--数据剖析--算法精解 * 算法君:http://www.suanfajun.com */ #include <iostream> #include <iomanip> using namespace std; void swap(int &x, int &y) { int temp = x; x = y; y = temp; } void insertion(int a[], int sz) { for(int i=1; i < sz; i++) { int j = i; while(j > 0 && (a[j] < a[j-1])) { swap(a[j], a[j-1]); j--; } cout << endl; for (int k = 0; k < sz; k++) cout << setw(3) << a[k]; } } int main() { int a[] = { 15, 9, 8, 1, 4, 11, 7, 12, 13, 6, 5, 3, 16, 2, 10, 14}; int size = sizeof(a)/sizeof(int); for (int i = 0; i < size; i++) cout << setw(3) << a[i]; insertion(a, size); cout << endl; return 0; } |

