1.快速排序的基本思想
交换排序的基本思想是:两两比较待排序记录(数据表)的关键字(排序码),发现两个记录的次序相反时即进行交换,直到没有反序的记录为止。主要包括冒泡排序和快速排序。
将所要进行排序的数分为左右两个部分,其中一部分的所有数据都比另外一 部分的数据小,然后将所分得的两部分数据进行同样的划分,重复执行以上的划分操作,直 到所有要进行排序的数据变为有序为止。
快速排序是一种分而治之的算法,通过递归的方式将数据依次分解为包含较小元素和较大元素的不同子序列。该算法不断重复这个步骤知道所有的数据都是有序的。
这个算法首先在数据列表中选择一个元素作为基准值(pivot)。数据的排序围绕基准值进行,将列表中小于基准值的元素一到数组的底部,将大于基准值的元素移动的数组的顶部。
2.快速排序的步骤
(1)快速排序步骤
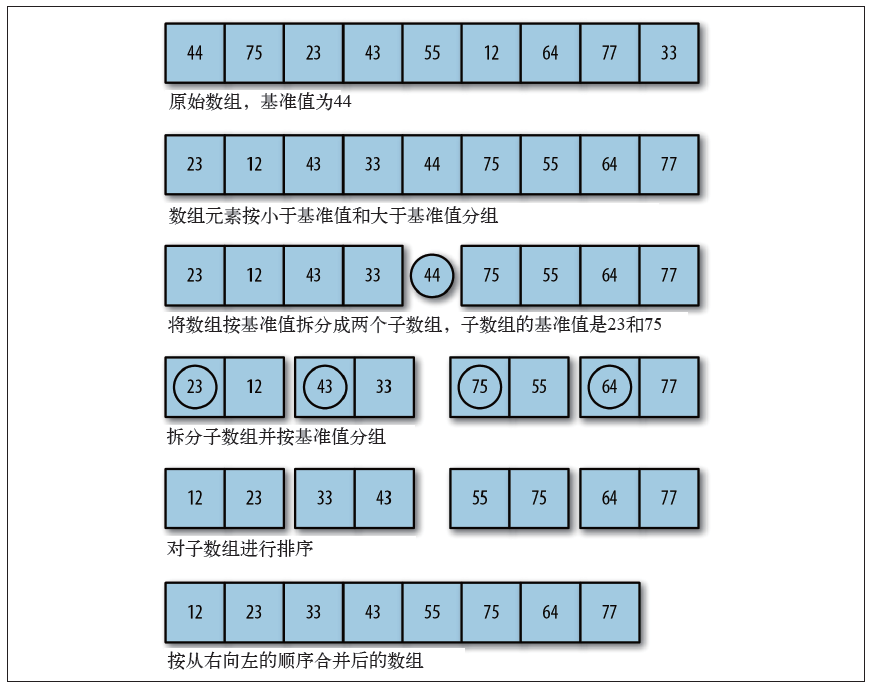
a.选择一个基准元素,将列表分割成两个子序列;
b.对列表重新排序,将所有小于基准值的元素放在基准值的前面,所有大于基准值的元素放在基准值的后面
c.分别对较小元素的子序列和较大元素的子序列重负步骤1,2。直到序列完成。
快速排序示意图
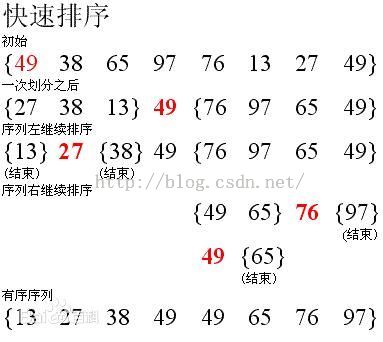
(2)快速排序举例
可能仅根据基本思想对快速排序的认识并不深,接下来以对n个无序数列A[0], A[1]…, A[n-1]采用快速排序方法进行升序排列为例进行讲解。
快速排序示意图
a.定义两个变量low和high,将low、high分别设置为要进行排序的序列的起始元素和最后一个元素的下标。第一次,low和high的取值分别为0和n-1,接下来的每次取值由划分得到的序列起始元素和最后一个元素的下标来决定。
b.定义一个变量key,接下来以key的取值为基准将数组A划分为左右两个部分,通 常,key值为要进行排序序列的第一个元素值。第一次的取值为A[0],以后毎次取值由要划 分序列的起始元素决定。
c.从high所指向的数组元素开始向左扫描,扫描的同时将下标为high的数组元素依次与划分基准值key进行比较操作,直到high不大于low或找到第一个小于基准值key的数组元素,然后将该值赋值给low所指向的数组元素,同时将low右移一个位置。
d.如果low依然小于high,那么由low所指向的数组元素开始向右扫描,扫描的同时将下标为low的数组元素值依次与划分的基准值key进行比较操作,直到low不小于high或找到第一个大于基准值key的数组元素,然后将该值赋给high所指向的数组元素,同时将high左移一个位置。
e.重复步骤(3) (4),直到low的植不小于high为止,这时成功划分后得到的左右两部分分别为A[low……pos-1]和A[pos+1……high],其中,pos下标所对应的数组元素的值就是进行划分的基准值key,所以在划分结束时还要将下标为pos的数组元素赋值 为 key。
f.将划分得到的左右两部分A[low……pos-1]和A[pos+1……high]继续采用以上操作步骤进行划分,直到得到有序序列为止。
3.快速排序分析
快速排序是一个递归算法,平均时间复杂度为O(nlog(n)),inplace操作,需要最小的额外内存。
(1)时间复杂度
当数据有序时,以第一个关键字为基准分为两个子序列,前一个子序列为空,此时执行效率最差。
而当数据随机分布时,以第一个关键字为基准分为两个子序列,两个子序列的元素个数接近相等,此时执行效率最好。
所以,数据越随机分布时,快速排序性能越好;数据越接近有序,快速排序性能越差。
(2)空间复杂度
快速排序在每次分割的过程中,需要 1 个空间存储基准值。而快速排序的大概需要 Nlog2N次 的分割处理,所以占用空间也是Nlog2N 个。
(3)算法稳定性
在快速排序中,相等元素可能会因为分区而交换顺序,所以它是不稳定的算法。
4.快速排序算法C语言源代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 | /** * 算法君:一个专业的算法学习分享网站 * 算法君:专业分享--数据剖析--算法精解 * 算法君:http://www.suanfajun.com */ #include <stdio.h> #include <stdlib.h> #define N 6 int partition(int arr[], int low, int high){ int key; key = arr[low]; while(low<high){ while(low <high && arr[high]>= key ) high--; if(low<high) arr[low++] = arr[high]; while( low<high && arr[low]<=key ) low++; if(low<high) arr[high--] = arr[low]; } arr[low] = key; return low; } void quick_sort(int arr[], int start, int end){ int pos; if (start<end){ pos = partition(arr, start, end); quick_sort(arr,start,pos-1); quick_sort(arr,pos+1,end); } return; } int main(void){ int i; int arr[N]={32,12,7, 78, 23,45}; printf("排序前 \n"); for(i=0;i<N;i++) printf("%d\t",arr[i]); quick_sort(arr,0,N-1); printf("\n 排序后 \n"); for(i=0; i<N; i++) printf("%d\t", arr[i]); printf ("\n"); system("pause"); return 0; } |
4.快速排序算法C++源代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 | /** * 算法君:一个专业的算法学习分享网站 * 算法君:专业分享--数据剖析--算法精解 * 算法君:http://www.suanfajun.com */ #include <iostream> #include <iomanip> using namespace std; #define SIZE 9 /* swap a[i] and a[j] */ void swap(int a[], int i, int j) { int temp; temp = a[i]; a[i] = a[j]; a[j] = temp; } void print(const int arr[]) { for(int i=0;i < SIZE; i++) { cout << setw(3) << arr[i]; } cout << endl; } /* sort arr[left]...arr[right] into increasing order */ void qsort(int a[], int left_index, int right_index) { int left, right, pivot; if(left_index >= right_index) return; left = left_index; right = right_index; // 枢轴选择 pivot selection pivot = a[(left_index + right_index) /2]; // 分割 partition while(left <= right) { while(a[left] < pivot) left++; while(a[right] > pivot) right--; if(left <= right) { swap(a,left,right); left++; right--; } print(a); } // 递归 recursion qsort(a,left_index,right); qsort(a,left,right_index); } int main() { int a[SIZE]={1, 12, 5, 26, 7, 14, 3, 7, 2}; print(a); qsort(a,0,SIZE-1); } |

