常用12大排序算法之九：基数排序(LSD+MSD)-分配式排序-桶子法排序

2017-04-22 23:05 阅读 5,601 次 评论 0 条

1.基数排序算法简介

基数排序（radix sort）属于“分配式排序”（distribution sort），又称“桶子法”（bucket sort）或bin sort，顾名思义，它是透过键值的部份资讯，将要排序的元素分配至某些“桶”中，藉以达到排序的作用，基数排序法是属于稳定性的排序，其时间复杂度为O (nlog(r)m)，其中r为所采取的基数，而m为堆数，在某些时候，基数排序法的效率高于其它的稳定性排序法。

基数排序（radix sorting）将所有待比较数值(正整数)统一为同样的数位长度，数位较短的数前面补零。 然后 从最低位开始，依次进行一次排序。这样从最低位排序一直到最高位排序完成以后， 数列就变成一个有序序列。

假设我们有一些二元组(a,b)，要对它们进行以a为首要关键字，b的次要关键字的排序。我们可以先把它们先按照首要关键字排序，分成首要关键字相同的若干堆。然后，在按照次要关键值分别对每一堆进行单独排序。最后再把这些堆串连到一起，使首要关键字较小的一堆排在上面。按这种方式的基数排序称为MSD(Most Significant Dight)排序。第二种方式是从最低有效关键字开始排序，称为LSD(Least Significant Dight)排序。首先对所有的数据按照次要关键字排序，然后对所有的数据按照首要关键字排序。要注意的是，使用的排序算法必须是稳定的，否则就会取消前一次排序的结果。由于不需要分堆对每堆单独排序，LSD方法往往比MSD简单而开销小。下文介绍的方法全部是基于LSD的。

基数排序的简单描述就是将数字拆分为个位十位百位，每个位依次排序。因为这对算法稳定要求高，所以我们对数位排序用到上一个排序方法计数排序。因为基数排序要经过d (数据长度)次排序， 每次使用计数排序， 计数排序的复杂度为 On),  d 相当于常量和N无关，所以基数排序也是 O(n)。基数排序虽然是线性复杂度， 即对n个数字处理了n次，但是每一次代价都比较高， 而且使用计数排序的基数排序不能进行原地排序，需要更多的内存， 并且快速排序可能更好地利用硬件的缓存， 所以比较起来，像快速排序这些原地排序算法更可取。对于一个位数有限的十进制数，我们可以把它看作一个多元组，从高位到低位关键字重要程度依次递减。可以使用基数排序对一些位数有限的十进制数排序。

例如我们将一个三位数分成，个位，十位，百位三部分。我们要对七个三位数来进行排序，依次对其个位，十位，百位进行排序，如下图：

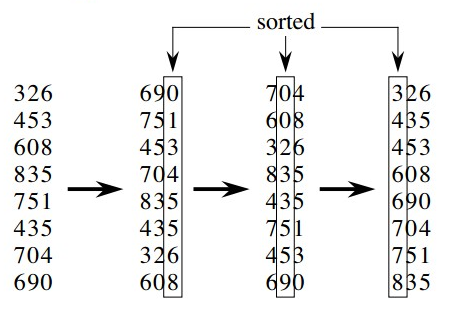
基数排序算法

很显然，每一位的数的大小都在[0，9]中，对于每一位的排序用计数排序再适合不过。

 

2.基数排序算法的基本原理

基数排序（以整形为例），将整形10进制按每位拆分，然后从低位到高位依次比较各个位。主要分为两个过程：

(1)分配——先从个位开始，根据位值(0-9)分别放到0~9号桶中（比如53,个位为3，则放入3号桶中）；

(2)收集——再将放置在0~9号桶中的数据按顺序放到数组中；

重复(1)(2)过程，从个位到最高位（比如32位无符号整形最大数4294967296，最高位10位）。

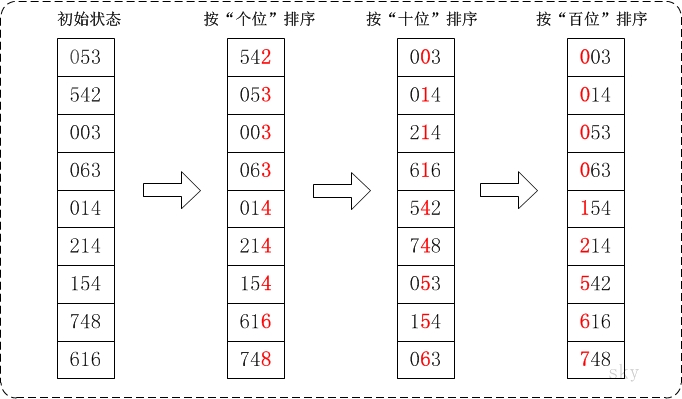
基数排序算法

 

3.基数排序算法基本步骤

举例分析：待排序数组[62,14,59,88,16]简单点五个数字

（1）分配10个桶,桶编号为0-9,以个位数数字为桶编号依次入桶,变成下边这样

|  0  |  0  | 62 |  0  | 14 |  0  | 16 |  0  |  88 | 59 |

|  0  |  1  |  2  |  3  |  4 |  5  |  6  |  7  |  8  |  9  |桶编号

（2）将桶里的数字顺序取出来

输出结果:[62,14,16,88,59]

（3）再次入桶,不过这次以十位数的数字为准,进入相应的桶,变成下边这样:

由于前边做了个位数的排序,所以当十位数相等时,个位数字是由小到大的顺序入桶的,就是说,入完桶还是有序

|  0  | 14,16 |  0  |  0  |  0  | 59 | 62  | 0  | 88  |  0  |

|  0  |  1      |  2  |  3  |  4  |  5  |  6  |  7  |  8  |  9  |桶编号

 因为没有大过100的数字,没有百位数,所以到这排序完毕。

（4）顺序取出即可

最后输出结果:[14,16,59,62,88]

 

4.基数排序算法复杂度分析

（1）平均时间复杂度：O(dn)(d即表示整形的最高位数)；

（2）空间复杂度：O(10n) （10表示0~9，用于存储临时的序列）；

（3）稳定性：稳定。

 

5.基数排序算法C语言源代码

基数排序算法C语言源代码
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
/**
* 算法君：一个专业的算法学习分享网站
* 算法君：专业分享--数据剖析--算法精解
* 算法君：http://www.suanfajun.com
*/
 
 
#include <stdio.h>
#include <assert.h>
#include <stdlib.h>
#include <time.h>
 
#define RADIXCOUNT 10  //桶的个数，桶号：0 1 2 ..... 9
#define RANDMAX 100000 //随机数的最大值加1+
 
struct Node {
    int value;
    struct Node *next;
};
 
struct Queue {
    struct Node *head;
    struct Node *tail;
};
 
//利用伪随机数填充数组array
void getRandArray(int array[], int size)
{
    assert(array != NULL && size > 0);
 
    srand((unsigned) time(NULL));
    int i = 0;
    for (i = 0; i < size; ++i) {
        //产生RANDMAX以内的伪随机数
        array[i] = rand() % RANDMAX;
    }
}
 
//基数排序，按从小到大的顺序进行排列
void radixSort(int array[], int size)
{
    assert(array != NULL && size > 0);
 
    struct Queue bucket[RADIXCOUNT];
    int i = 0;
    for (i = 0; i < RADIXCOUNT; ++i) {
        bucket[i].head = NULL;
        bucket[i].tail = NULL;
    }
 
    int maxLength = getMaxLength(array, size);
    int dividend = 1;
    for (i = 0; i < maxLength; ++i) {
        distributeNumbers(array, size, bucket, dividend);
        rearrangeArray(array, size, bucket);
        dividend *= 10;
        // printArray(array, size);
    }
}
 
//获取数组array中最大数的长度（位数）
int getMaxLength(int array[], int size)
{
    assert(array != NULL && size > 0);
 
    int max = array[0];
    int i = 0;
    for (i = 1; i < size; ++i) {
        if (max < array[i]) {
            max = array[i];
        }
    }
 
    int length = 1;
    while ((max /= 10) != 0) {
        ++length;
    }
    return length;
}
 
//把数组array中的数放到对应的桶中,桶的底层是用链式队列实现的
void distributeNumbers(int array[], int size, struct Queue bucket[], int dividend)
{
    assert(array != NULL && size > 0 && bucket != NULL && dividend > 0);
 
    int radixValue = 0;
    struct Node *node;
    int i = 0;
    for (i = 0; i < size; ++i) {
        //把array[i]放到下标为radixValue的桶中
        radixValue = (array[i] / dividend) % 10;
        node = (struct Node *) malloc(sizeof(struct Node));
        node -> value = array[i];
        node -> next = NULL;
        if (bucket[radixValue].head == NULL) {
            bucket[radixValue].head = node;
            bucket[radixValue].tail = node;
        } else {
            bucket[radixValue].tail -> next = node;
            bucket[radixValue].tail = node;
        }
    }
}
 
//把桶0..9中的数按放入桶中的先后次序放回到数组array中
void rearrangeArray(int array[], int size, struct Queue bucket[])
{
    assert(array != NULL && size > 0 && bucket != NULL);
 
    struct Node *pointer = NULL;
    int arrayIndex = 0;
    int listIndex = 0;
    for (listIndex = 0; listIndex < RADIXCOUNT; ++listIndex) {
        while (bucket[listIndex].head != NULL) {
            array[arrayIndex++] = bucket[listIndex].head -> value;
            pointer = bucket[listIndex].head;
            bucket[listIndex].head = bucket[listIndex].head -> next;
            free(pointer);
        }
    }
}
 
// 打印输出数组
void printArray(int array[], int size)
{
    assert(array != NULL && size > 0);
 
    int i = 0;
    for (i = 0; i < size; ++i) {
        printf("%d ", array[i]);
    }
    printf("\n\n");
}
 
//判断数组array是否已经是有序的
void isSorted(int array[], int size)
{
    assert(array != NULL && size > 0);
 
    int unsorted = 0;
    int i = 0;
    for (i = 1; i < size; ++i) {
        if (array[i] < array[i - 1]) {
            unsorted = 1;
            break;
        }
    }
 
    if (unsorted) {
        printf("the array is unsorted!\n");
    } else {
        printf("the array is sorted!\n");
    }
}
 
int main(int argc, char const *argv[])
{
    int size = 0;
    scanf("%d", &size);
    assert(size > 0);
 
    int *array = (int *)calloc(size, sizeof(int));
    getRandArray(array, size);
    printArray(array, size);
 
    radixSort(array, size);
    printArray(array, size);
    isSorted(array, size);
 
    free(array);
    return 0;
}

 

6.基数排序算法C++源代码

（1）基于LSD的基数排序算法

基于LSD的基数排序算法C++源代码
C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
/**
* 算法君：一个专业的算法学习分享网站
* 算法君：专业分享--数据剖析--算法精解
* 算法君：http://www.suanfajun.com
*/
 
 
// 基于LSD的基数排序算法
#include <iostream>
 
using namespace std;
const int MAX = 10;
 
void print(int *a,int sz) {
    for(int i = 0; i < sz; i++)
        cout << a[i] << " ";
    cout << endl;
}
 
void RadixSortLSD(int *a, int arraySize)
{
    int i, bucket[MAX], maxVal = 0, digitPosition =1 ;
    for(i = 0; i < arraySize; i++) {
        if(a[i] > maxVal) maxVal = a[i];
    }
 
    int pass = 1;  // used to show the progress
    /* maxVal: this variable decide the while-loop count
         if maxVal is 3 digits, then we loop through 3 times */
    while(maxVal/digitPosition > 0) {
        /* reset counter */
        int digitCount[10] = {0};
 
        /* count pos-th digits (keys) */
        for(i = 0; i < arraySize; i++)
            digitCount[a[i]/digitPosition%10]++;
 
        /* accumulated count */
        for(i = 1; i < 10; i++)
            digitCount[i] += digitCount[i-1];
 
        /* To keep the order, start from back side */
        for(i = arraySize - 1; i >= 0; i--)
            bucket[--digitCount[a[i]/digitPosition%10]] = a[i];
 
        /* rearrange the original array using elements in the bucket */
        for(i = 0; i < arraySize; i++)
            a[i] = bucket[i];
 
        /* at this point, a array is sorted by digitPosition-th digit */
        cout << "pass #" << pass++ << ": ";
        print(a,arraySize);
 
        /* move up the digit position */
        digitPosition *= 10;
    }
}
 
int main()
{
    int a[] = {170, 45, 75, 90, 2, 24, 802, 66};
    const size_t sz = sizeof(a)/sizeof(a[0]);
 
    cout << "pass #0: ";
    print(a,sz);
    RadixSortLSD(&a[0],sz);
    return 0;
}

（2）基于数组的基数排序算法

基于数组的基数排序算法C++源代码
C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
/**
* 算法君：一个专业的算法学习分享网站
* 算法君：专业分享--数据剖析--算法精解
* 算法君：http://www.suanfajun.com
*/
 
 
// 基于数组的基数排序算法
#include<iostream>
#include <vector>
 
using namespace std;
 
int maxbit(int data[],int n)
{
    int d=1;
    for(int i=0;i<n;i++)
    {
        int c=1;
        int p=data[i];
        while(p/10)
        {
            p=p/10;
            c++;
        }
        if(c>d)
            d=c;
    }
    return d;
}
 
void RadixSort(int data[],int n)
{
    int d=maxbit(data,n);
    int r=1;
    int tmp[10];
    int count[10];
 
    for(int i=0;i<d;i++)
    {
 
        for(int i=0;i<10;i++)//装桶之前要先清桶
            count[i]=0;
        for(i=0;i<n;i++) //记录每个桶的记录数
        {
            int k=data[i]/r;
            int q=k%10;
            count[q]++;
        }
        for(i=1;i<10;i++)//计算位置
        {
            count[i]+=count[i-1];
            //cout<<count[i]<<" ";
        }
        for(int j=n-1;j>=0;j--)
        {
            int p=data[j]/r;
            int s=p%10;
            tmp[count[s]-1]=data[j];
            count[s]--;
            //cout<<data[j]<<" ";
        }
        for(i=0;i<n;i++)
        {
            data[i]=tmp[i];
            //cout<<tmp[i]<<" ";
        }
    //    cout<<endl;
        r=r*10;
 
    }
 
}
int main()
{
    int data[10]={73, 22, 93, 43, 55, 14, 28, 65, 39, 81};
 
    cout<<"基数排序c++实现"<<endl;
    //cout<<maxbit(data,10)<<endl;
    cout<<"排序之前的数值：";
    for(int i=0;i<10;i++)
        cout<<data[i]<<" ";
    cout<<endl;
    RadixSort(data,10);
    cout<<"排序之后的数值：";
        for(i=0;i<10;i++)
        cout<<data[i]<<" ";
    cout<<endl;
 
 
    return 0;
}

 

（3）基于静态链表的基数排序算法

基于静态链表基数排序算法C++源代码
C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
/**
* 算法君：一个专业的算法学习分享网站
* 算法君：专业分享--数据剖析--算法精解
* 算法君：http://www.suanfajun.com
*/
 
 
// 基于静态链表基数排序算法实现
#include <iostream>
using namespace std;
 
typedef struct list  //静态链表结构体类型
{
    int data;
    int next;
}List;
 
List d[10];        //将待排序数据构造成list类型的数组
List bucket[10];   //构造十个桶
 
int maxbit(int data[],int n)   //计算待排序数组元数的最长的位数
{
    int d=1;
    for(int i=0;i<n;i++)
    {
        int c=1;
        int p=data[i];
        while(p/10)
        {
            p=p/10;
            c++;
        }
        if(c>d)
            d=c;
    }
    return d;
}
void init(int data[],int n)  //清桶的过程，以及将临时的数组放到d【10】数组中
{
       int j=0;
 
        for(j=0;j<n;j++)
        {
            bucket[j].next=-1;
            bucket[j].data=j;
        }
        for(j=0;j<n;j++)
        {
          d[j].data=data[j];
          d[j].next=-1;
        }
}
void RadioSort(int data[],int n)   //基数排序的过程
{
 
    int p=maxbit(data,n);   //先求出最长的位数
    int r=1;
    for(int i=0;i<p;i++)   //执行装桶倒桶的次数
    {
        init(data,n);   //复位清桶的过程
        if(i!=0)   //第一次装桶的时候从小到大开始装，之后都从大到小装桶
        {
            for(int k=n-1;k>=0;k--)
            {
                int a=d[k].data/r;
                int b=a%10;
                d[k].next=bucket[b].next;
                bucket[b].next=k;
            }
        }
        else
        {
            for(int k=0;k<n;k++)
            {
                int a=d[k].data/r;
                int b=a%10;
                d[k].next=bucket[b].next;
                bucket[b].next=k;
            }
        }
 
        int c=0;
        for(int k=0;k<n;k++)   //倒桶的过程，将其放到data数组当中
        {
 
            if(bucket[k].next!=-1)
            {
                int p=bucket[k].next;
                data[c++]=d[p].data;
                while(d[p].next!=-1){
                        data[c++]=d[d[p].next].data;
                        p=d[p].next;
                }
            }
        }
        r=r*10;  //为了后面对十位数以及高位求当前位置上的数字
    }
}
int main()
{
    int data[10]={73, 22, 93, 43, 55, 14, 28, 65, 39, 81};  //待排序的数组
 
    cout<<"基于静态链表的基数排序c++实现"<<endl;
 
    //cout<<maxbit(data,10)<<endl;
    cout<<"排序之前的数值：";
    for(int i=0;i<10;i++)
        cout<<data[i]<<" ";
    cout<<endl;
 
    RadioSort(data,10);
 
    cout<<"排序之前的数值：";
    for(i=0;i<10;i++)
        cout<<data[i]<<" ";
    cout<<endl;
 
 
    return 0;
}

 

版权声明：本文著作权归原作者所有，欢迎分享本文，谢谢支持！
转载请注明：常用12大排序算法之九：基数排序(LSD+MSD)-分配式排序-桶子法排序 | 算法君
分类：数据结构 标签：,

发表评论


表情