1.二分(折半)插入排序法基本思想
设在顺序表中有一个对象序列V[0],V[1],…,V[n−1]。其中, V[0],V[1],…,V[i−1]是已经排好序的对象。在插入V[i]时,利用二分搜索法寻找V[i]的插入位置。关于二分搜索法在我的博文《查找searching》中有精彩论述,这里只是简要的说明一下二分搜索在二分插入排序中的应用。
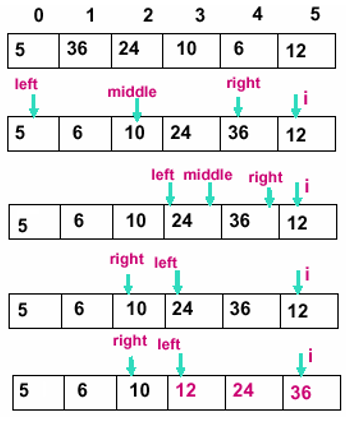
第一行是原始数据,第二行是假设已经排好了前i个数据,在排a[i]时,采用二分搜索(查找)的方法在前i个数据中找到合适的位置插入。下面几行是二分查找的步骤,每次将查找的范围缩小一半儿,直到找到合适位置为止,然后在该位置上插入a[i],其余数据往后移动一个位置。
2.二分插入排序算法分析
二分搜索比顺序搜索查找快,所以二分插入排序就平均性能来说比直接插入排序要快。
它所需的排序码比较次数与待排序对象序列的初始排列无关,仅依赖于对象个数。在插入第i个对象时,需要经过log2i+1次排序码比较,才能确定它应插入的位置。 将n个对象用折半插入排序所进行的排序码比较次数比较次数(KCN):∑n−1(log2i+1)≈nlog2n
二分插入排序是一个稳定的排序方法。
当n较大时,总排序码比较次数比直接插入排序的最坏情况要好得多,但比其最好情况要差。
在对象的初始排列已经按排序码排好序或接近有序时,直接插入排序比折半插入排序执行的排序码比较次数要少。折半插入排序的对象移动次数与直接插入排序相同,依赖于对象的初始排列。
3.二分(折半)插入排序法C语言源代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 | /** * 算法君:一个专业的算法学习分享网站 * 算法君:专业分享--数据剖析--算法精解 * 算法君:http://www.suanfajun.com */ #include<stdio.h> //二分查找-C语言实现 //基本思路:将排序好的数据存放到数组里(不能是链表) // 这只前中后标签,与中间元素比,若小于就将后变为原来的中 // 继续计算中,比较,循环,直至等于中,或循环结束。 int binsearch(int *sortedSeq, int seqLength, int keyData); int main() { int array[] = { 1, 2, 3, 4, 5, 6, 7, 8, 9 }; int location; int target = 4; location = binsearch(array, 9, target); printf("%d\n", location); return 0; } int binsearch(int *sortedSeq, int seqLength, int keyData) { int low = 0, mid, high = seqLength - 1; while (low <= high) { mid = (low + high) / 2;//奇数,无论奇偶,有个值就行 if (keyData < sortedSeq[mid]) { high = mid - 1;//是mid-1,因为mid已经比较过了 } else if (keyData > sortedSeq[mid]) { low = mid + 1; } else { return mid; } } return -1; } |
4.二分(折半)插入排序法C++源代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 | /** * 算法君:一个专业的算法学习分享网站 * 算法君:专业分享--数据剖析--算法精解 * 算法君:http://www.suanfajun.com */ #define size 5 #include<iostream> using namespace std; int main() { int i,j; float t,a[size]; for (i=0;i<size;i++) //从键盘上为数组赋值 { cout<<"a["<<i<<"]="; cin>>a[i]; } for (i=0;i<size-1;i++) //使用冒泡排序法对数组按从小到大顺序排序 for (j=i+1;j<size;j++) if (a[i]>a[j]) { t=a[i]; a[i]=a[j]; a[j]=t; } for (i=0;i<size;i++) //显示排序结果 cout<<a[i]<<" "; cout<<endl; int value; int found; //找到为1,否则为0 int low,high,mid; for (i=1;i<=3;i++) { cout<<"value="; cin>>value; //输入要查找的数据 found=0; //二分法(又叫折半查找法)查找数组a low=0; high=size-1; while(low<=high) { mid=(high+low)/2; if (a[mid]==value) { found=1; break; } if (a[mid]<value) low=mid+1; //mid往右移动 else high=mid-1; //mid往左移动右逢源 } if (found) //fond的初始值为0,一旦找到,found变量被置1,引发此条件语句,从而输出找到的结果,否则告知用户找不到。 cout<<"The valu found at:a["<<mid<<"]="<<a[mid]<<endl; else cout<<"The "<<value<<" is not found!"<<endl; } return 0; } |

