常用12大排序算法之八：归并排序（递归+非递归）

2017-04-22 22:01 阅读 5,221 次 评论 0 条

1.归并排序的基本思想

归并，是将两个或两个以上的有序表合并成一个新的有序表。

对象序列initList中两个有序表V[1]…V[m]和V[m+1]…V[n]。它们可归并成一个有序表,存于另一对象序列mergedList的V[1]…V[n]中。这种归并方法称为两路归并(2- way merging) 。

归并排序的特点和思想：

（1）采用分而治之（divide and conquer）的策略；

（2）小的数据表排序比大的数据表要快；

（3）从两个已经排好序的数据表中构造一个排好序的数据表要比从两个未排序的书记表中构造要少许多步骤；

（4）它是一个稳定的排序算法；

（5）可以从递归、迭代两种思想实现。

 

2.归并排序的步骤

迭代的归并排序算法就是利用两路归并过程进行排序的。其基本思想是：假设初始序列有n个对象，首先把它看n个长度为1的有序子序列,两两并归,重复上述操作,直到得到一个序列。特点是辅助空间占用多；稳定。

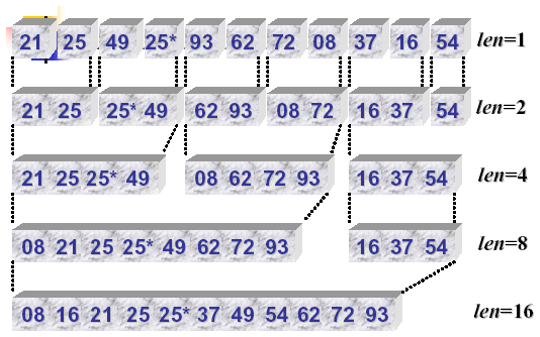
迭代的归并排序算法

与快速排序类似，归并排序算法也可以利用划分为子序列的方法递归实现。在递归的归并排序算法中，首先要把整个待排序序列划分为两个长度大致相等的部分,左子表和右子表。对子表分别递归地进行排序, 然后再把排好序的两个子表并归。特点是链表的归并排序方法的递归深度为O(log2n)，对象排序码的比较次数为O(nlog2n)；稳定。

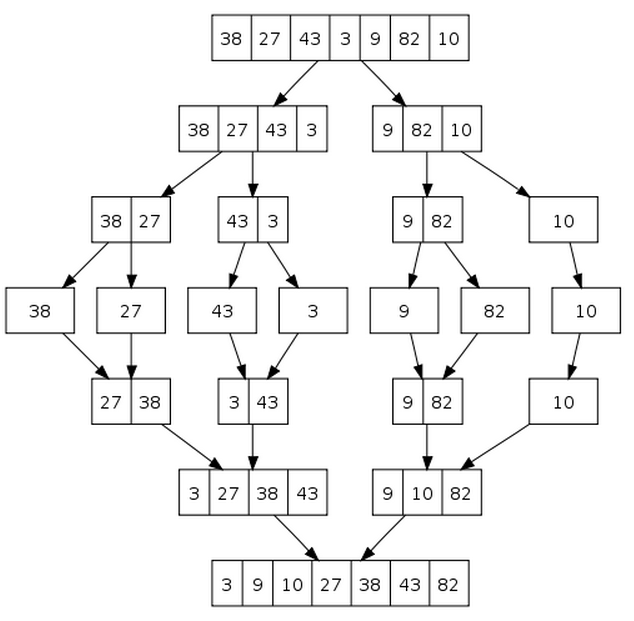
递归的归并排序算法

（1）申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列；

（2）设定两个指针，最初位置分别为两个已经排序序列的起始位置；

（3）比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置；

（4）重复步骤3直到某一指针超出序列尾；

（5）将另一序列剩下的所有元素直接复制到合并序列尾。

 

3.归并排序算法复杂度分析

（1）时间复杂度为O(nlogn) 这是该算法中最好、最坏和平均的时间性能；

（2）空间复杂度为 O(n)；

（3）比较操作的次数介于(nlogn) / 2和nlogn - n + 1；

（4）赋值操作的次数是(2nlogn)。归并算法的空间复杂度为：0 (n)；

（5）归并排序比较占用内存，但却是一种效率高且稳定的算法。

 

4.归并算法C语言源代码

归并排序算法C语言源代码
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
/**
* 算法君：一个专业的算法学习分享网站
* 算法君：专业分享--数据剖析--算法精解
* 算法君：http://www.suanfajun.com
*/
 
 
 
#include <stdlib.h>
#include <stdio.h>
void Merge(int sourceArr[],int tempArr[], int startIndex, int midIndex, int endIndex)
{
    int i = startIndex, j=midIndex+1, k = startIndex;
    while(i!=midIndex+1 && j!=endIndex+1)
    {
        if(sourceArr[i] > sourceArr[j])
            tempArr[k++] = sourceArr[j++];
        else
            tempArr[k++] = sourceArr[i++];
    }
    while(i != midIndex+1)
        tempArr[k++] = sourceArr[i++];
    while(j != endIndex+1)
        tempArr[k++] = sourceArr[j++];
    for(i=startIndex; i<=endIndex; i++)
        sourceArr[i] = tempArr[i];
}
//内部使用递归
void MergeSort(int sourceArr[], int tempArr[], int startIndex, int endIndex)
{
    int midIndex;
    if(startIndex < endIndex)
    {
        midIndex = (startIndex + endIndex) / 2;
        MergeSort(sourceArr, tempArr, startIndex, midIndex);
        MergeSort(sourceArr, tempArr, midIndex+1, endIndex);
        Merge(sourceArr, tempArr, startIndex, midIndex, endIndex);
    }
}
int main(int argc, char * argv[])
{
    int a[8] = {50, 10, 20, 30, 70, 40, 80, 60};
    int i, b[8];
    MergeSort(a, b, 0, 7);
    for(i=0; i<8; i++)
        printf("%d ", a[i]);
    printf("\n");
    return 0;
}

 

 

5.归并算法C++源代码

（1）递归归并排序算法

递归归并排序算法C++源代码
C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
/**
* 算法君：一个专业的算法学习分享网站
* 算法君：专业分享--数据剖析--算法精解
* 算法君：http://www.suanfajun.com
*/
 
 
 
#include<iostream>
using namespace std;
 
void merge(int *data, int start, int mid, int end, int *result)
{
    int i, j, k;
    i = start;
    j = mid + 1;                        //避免重复比较data[mid]
    k = 0;
    while (i <= mid && j <= end)        //数组data[start,mid]与数组(mid,end]均没有全部归入数组result中去
    {
        if (data[i] <= data[j])         //如果data[i]小于等于data[j]
            result[k++] = data[i++];    //则将data[i]的值赋给result[k]，之后i,k各加一，表示后移一位
        else
            result[k++] = data[j++];    //否则，将data[j]的值赋给result[k]，j,k各加一
    }
    while (i <= mid)                    //表示数组data(mid,end]已经全部归入result数组中去了，而数组data[start,mid]还有剩余
        result[k++] = data[i++];        //将数组data[start,mid]剩下的值，逐一归入数组result
    while (j <= end)                    //表示数组data[start,mid]已经全部归入到result数组中去了，而数组(mid,high]还有剩余
        result[k++] = data[j++];        //将数组a[mid,high]剩下的值，逐一归入数组result
    for (i = 0; i < k; i++)             //将归并后的数组的值逐一赋给数组data[start,end]
        data[start + i] = result[i];    //注意，应从data[start+i]开始赋值
}
 
void merge_sort(int *data, int start, int end, int *result)
{
    if (start < end)
    {
        int mid = (start + end) / 2;
        merge_sort(data, start, mid, result);                    //对左边进行排序
        merge_sort(data, mid + 1, end, result);                  //对右边进行排序
        merge(data, start, mid, end, result);                    //把排序好的数据合并
    }
}
 
void amalgamation(int *data1, int *data2, int *result)
{
    for (int i = 0; i < 10; i++)
        result[i] = data1[i];
    for (int i = 0; i < 10; i++)
        result[i + 10] = data2[i];
}
 
int main()
{
    int data1[10] = { 1,7,6,4,9,14,19,100,55,10 };
    int data2[10] = { 2,6,8,99,45,63,102,556,10,41 };
    int *result = new int[20];                              
    int *result1 = new int[20];
    amalgamation(data1, data2, result);
    for (int i = 0; i < 20; ++i)
        cout << result[i] << "  ";
    cout << endl;
    merge_sort(result, 0, 19, result1);
    for (int i = 0; i < 20; ++i)
        cout << result[i] << "  ";
    delete[]result;
    delete[]result1;
    return 0;
}

 

（2）非递归归并排序算法

非递归归并排序算法C++源代码
C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
/**
* 算法君：一个专业的算法学习分享网站
* 算法君：专业分享--数据剖析--算法精解
* 算法君：http://www.suanfajun.com
*/
 
 
 
#include<iostream>
#include<ctime>
#include<cstring>
#include<cstdlib>
using namespace std;
/**将a开头的长为length的数组和b开头长为right的数组合并n为数组长度，用于最后一组*/
void　Merge(int*　data,int　a,int　b,int　length,int　n){
　int　right;
　if(b+length-1 >= n-1)　right = n-b;
　else　right = length;
　int*　temp = new　int[length+right];
　int　i=0, j=0;
　while(i<=length-1 && j<=right-1){
    　if(data[a+i] <= data[b+j]){
    　    temp[i+j] = data[a+i];i++;
      }
    　else{
        temp[i+j] = data[b+j];
        j++;
      }
　}
　if(j == right){//a中还有元素，且全都比b中的大,a[i]还未使用
　  memcpy(temp + i + j, data + a + i, (length - i) * sizeof(int));
　}
  else if(i == length){
      memcpy(temp + i + j, data + b + j, (right - j)*sizeof(int));
  }
　memcpy(data+a, temp, (right + length) * sizeof(int));
　delete [] temp;
}
 
void　MergeSort(int*　data, int　n){
　int　step = 1;
　while(step < n){
    　for(int　i=0; i<=n-step-1; i+=2*step)
    　    Merge(data, i, i+step, step, n);
    //将i和i+step这两个有序序列进行合并
    //序列长度为step
    //当i以后的长度小于或者等于step时，退出
    　step*=2; //在按某一步长归并序列之后，步长加倍
　}
}
 
int　main(){
　int　n;
　cin>>n;
　int*　data = new　int[n];
　if(!data)　exit(1);
　int　k = n;
　while(k--){
　    cin>>data[n-k-1];
　}
　clock_t　s = clock();
　MergeSort(data, n);
　clock_t　e = clock();
　k=n;
　while(k--){
　    cout<<data[n-k-1]<<' ';
　}
　cout<<endl;
　cout<<"the algorithm used"<<e-s<<"miliseconds."<<endl;
　delete　data;
　return　0;
}

（3）二路递归归并排序算法

二路递归归并排序算法C++源代码
C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
/**
* 算法君：一个专业的算法学习分享网站
* 算法君：专业分享--数据剖析--算法精解
* 算法君：http://www.suanfajun.com
*/
 
 
 
#include <iostream>
using namespace std;
 
//将数组 a[low,mid] 与 a(mid,high] 合并（归并）
void Merge(int * a, int low, int mid, int high, int * temp)
{
    int i,j,k;
    i = low;
    j = mid + 1;//避免重复比较a[mid]
    k = 0;
    while (i <= mid && j <= high)//数组a[low,mid]与数组(mid,high]均没有全部归入数组temp中去
    {
        if(a[i] <= a[j])        //如果a[i]小于等于a[j]
            temp[k++] = a[i++]; //则将a[i]的值赋给temp[k]，之后i,k各加一，表示后移一位
        else
            temp[k++] = a[j++]; //否则，将a[j]的值赋给temp[k]，j,k各加一
    }
    while(i <= mid)             //表示数组a(mid,high]已经全部归入temp数组中去了，而数组a[low,mid]还有剩余
        temp[k++] = a[i++];     //将数组a[low,mid]剩下的值，逐一归入数组temp
    while(j <= high)           //表示数组a[low,mid]已经全部归入到temp数组中去了，而数组(mid,high]还有剩余
        temp[k++] = a[j++];     //将数组a(mid,high]剩下的值，逐一归入数组temp
 
    for (i = 0; i < k; i++)     //将归并后的数组的值逐一赋给数组a[low,high]
        a[low+i] = temp[i];     //注意，应从a[low+i]开始赋值
}
 
//二路归并（递归实现）
void MergeSort(int * a, int low, int high, int * temp)
{
    if (low < high)
    {
        int mid = (low + high)/2;
        MergeSort(a,low,mid,temp);      //左边有序
        MergeSort(a,mid+1,high,temp);   //右边有序
        Merge(a,low,mid,high,temp);     //再将两个有序序列合并
    }
}
 
/*----------测试代码----------*/
int main()
{
    int a[] = {2,23,34,43,45,6,7,8,5,4,56,78,80,211,222,444,111};
    int La = sizeof(a)/sizeof(a[0]);
    int * p = new int[La];
    MergeSort(a,0,La-1,p);
    for (int i = 0; i < La; i++)
    {
        cout<<a[i]<<' ';
    }
    cout<<endl;
    delete []p;
}

 

 

 

版权声明：本文著作权归原作者所有，欢迎分享本文，谢谢支持！
转载请注明：常用12大排序算法之八：归并排序（递归+非递归） | 算法君
分类：数据结构 标签：, ,

发表评论


表情