常用12大排序算法之十一：计数排序算法（原理与代码实现）

2017-04-23 00:03 阅读 5,929 次 评论 0 条

1.计数排序简介

计数排序是一个非基于比较的排序算法，该算法于1954年由 Harold H. Seward 提出。它的优势在于在对一定范围内的整数排序时，它的复杂度为Ο(n+k)（其中k是整数的范围），快于任何比较排序算法。[1-2]  当然这是一种牺牲空间换取时间的做法，而且当O(k)>O(n*log(n))的时候其效率反而不如基于比较的排序（基于比较的排序的时间复杂度在理论上的下限是O(n*log(n)), 如归并排序，堆排序）。

 

2.计数排序算法的基本思想

计数排序对输入的数据有附加的限制条件：（1）输入的线性表的元素属于有限偏序集S；（2）设输入的线性表的长度为n，|S|=k（表示集合S中元素的总数目为k），则k=O(n)。

在这两个条件下，计数排序的复杂性为O(n)。

计数排序的基本思想是对于给定的输入序列中的每一个元素x，确定该序列中值小于x的元素的个数（此处并非比较各元素的大小，而是通过对元素值的计数和计数值的累加来确定）。一旦有了这个信息，就可以将x直接存放到最终的输出序列的正确位置上。例如，如果输入序列中只有17个元素的值小于x的值，则x可以直接存放在输出序列的第18个位置上。当然，如果有多个元素具有相同的值时，我们不能将这些元素放在输出序列的同一个位置上，因此，上述方案还要作适当的修改。

 

3.计数排序算法的基本过程

假设输入的线性表L的长度为n，L=L1,L2,..,Ln；线性表的元素属于有限偏序集S，|S|=k且k=O(n)，S={S1,S2,..Sk}；则计数排序可以描述如下：

（1）扫描整个集合S，对每一个Si∈S，找到在线性表L中小于等于Si的元素的个数T(Si)；

（2）扫描整个线性表L，对L中的每一个元素Li，将Li放在输出线性表的第T(Li)个位置上，并将T(Li)减1。

 

4.计数排序算法的算法流程

（1）找出待排序的数组中最大和最小的元素；
（2）统计数组中每个值为i的元素出现的次数，存入数组C的第i项；
（3）对所有的计数累加（从C中的第一个元素开始，每一项和前一项相加）；
（4）反向填充目标数组：将每个元素i放在新数组的第C(i)项，每放一个元素就将C(i)减去1。

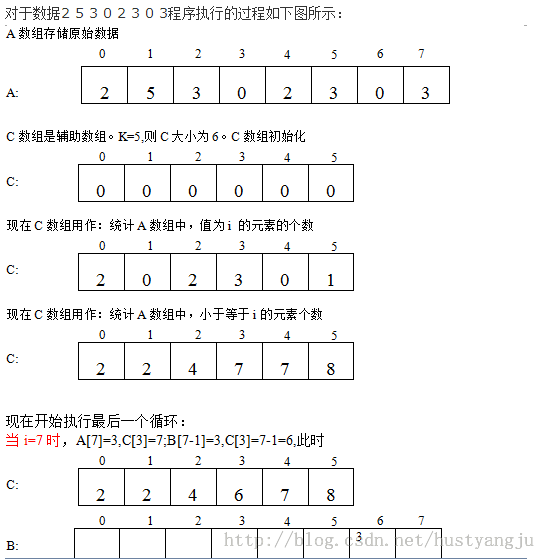
计数排序

 

5.计数排序算法C语言源代码

计数排序算法C语言源代码
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
/**
* 算法君：一个专业的算法学习分享网站
* 算法君：专业分享--数据剖析--算法精解
* 算法君：http://www.suanfajun.com
*/
 
 
#include <stdio.h>
#include <stdlib.h>
 
#define random(x)    (rand()%(x))
#define NUM 100      //产生100个随机数
#define MAXNUM 200   //待排序的数字范围是0-200
 
void countingSort(int A[], int n, int k){
    int *ptemp, *pout;
    int i;
    ptemp = (int *)malloc(sizeof(int)*k);
    pout = (int *)malloc(sizeof(int)*n);
    for (i = 0; i < k; i++)
        ptemp[i] = 0;
    for (i = 0; i < n; i++)
        ptemp[A[i]] += 1;
    for (i = 1; i < k; i++)
        ptemp[i] = ptemp[i - 1] + ptemp[i];
    for (i = n - 1; i >= 0; i--)
    {
        pout[ptemp[A[i]] - 1] = A[i];
        ptemp[A[i]] -= 1;
    }
    for (i = 0; i < n; i++)
        A[i] = pout[i];
    free(ptemp);
    free(pout);
}
 
void printArray(int A[], int n){
    int i = 0;
    for (i = 0; i < n; i++){
        printf("%4d", A[i]);
    }
    printf("\n");
}
void main()
{
    int A[NUM];
    int i;
    for (i = 0; i < NUM; i++)
        A[i] = random(MAXNUM);
    printf("before sorting:\n");
    printArray(A, NUM);
    countingSort(A, NUM, MAXNUM);
    printf("after sorting:\n");
    printArray(A, NUM);
}

计数排序算法C语言源代码
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
/**
* 算法君：一个专业的算法学习分享网站
* 算法君：专业分享--数据剖析--算法精解
* 算法君：http://www.suanfajun.com
*/
 
 
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
 
// 打印输出数组
void print_arry(int *arr,int n)
{
    int i;
    for(i = 0; i<n; i++)
    {
        printf("%d ", arr[i]);
    }
    printf("\n");
}
 
// 计数排序
void count_sort(int *arr, int *sorted_arr, int n)
{
    int *count_arr = (int *)malloc(sizeof(int) * 100);
    int i;
    //初始化计数数组
    for(i = 0; i<100; i++)
        count_arr[i] = 0;
    //统计i的次数
    for(i = 0;i<n;i++)
        count_arr[arr[i]]++;
    //对所有的计数累加
    for(i = 1; i<100; i++)
        count_arr[i] += count_arr[i-1];
    //逆向遍历源数组（保证稳定性），根据计数数组中对应的值填充到先的数组中
    for(i = n; i>0; i--)
    {
        sorted_arr[count_arr[arr[i-1]]-1] = arr[i-1];
        count_arr[arr[i-1]]--;  
    }
    free(count_arr);
}
 
int main() {
    int n,i;
    printf ("待排序数组的大小 n=");
    scanf ("%d", &n);
    
    int *arr = (int *)malloc(sizeof(int) * n);
    int *sorted_arr = (int *)malloc(sizeof(int) * n);
    
    srand (time (0));
    for (i = 0; i<n; i++)
    {
        arr[i] = rand() % 100;
    }
    printf ("随机生成数值为0~99的数组...\n");
    printf ("初始化数组: ");
    print_arry(arr, n);
    count_sort(arr, sorted_arr, n);
    printf ("排序后的数组：");
    print_arry(sorted_arr, n);
    return 0;
    system ("pause");
    
}

计数排序算法C语言源代码
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
/**
* 算法君：一个专业的算法学习分享网站
* 算法君：专业分享--数据剖析--算法精解
* 算法君：http://www.suanfajun.com
*/
 
 
#include <stdio.h>
#include <stdlib.h>
#include <malloc.h>
#include <string.h>
 
/**************************************************************
*计数排序。
*参数：   data : 要排序的数组
*              size ：数组元素的个数
*              k      ：数组中元素数组最大值 +1 （这个需要+1）
*返回值： 成功0；失败-1.        
* ************************************************************/  
 
int cnt_sort(int* data, int size, int k)  
{  
    int* counts = NULL; /*计数数组*/  
    int* temp = NULL;   /*保存排序后的数组*/  
  
    
    if ((counts = (int *) malloc( k * sizeof(int))) == NULL)   /*申请数组空间*/
        return -1;  
    if ((temp = (int *) malloc( k * sizeof(int))) == NULL)  
        return -1;  
  
  
    for (int i = 0; i < k; i ++)   /*初始化计数数组*/  
    {
        counts[i] = 0;
    }
    
    for(int i = 0; i < size; i++)  /*数组中出现的元素，及出现次数记录*/
    {
        counts[data[i]] += 1;  
    }
  
    for (i = 1; i < k; i++)      /*调整元素计数中，加上前一个数*/  
    {
        counts[i] += counts[i - 1];  
    }
      
    for (i = size -1; i >= 0; i --)/*使用计数数组中的记录数值，来进行排序，排序后保存的temp*/
    {  
        temp[counts[data[i]] - 1] = data[i];  
        counts[data[i]] -= 1;  
    }        
  
    memcpy(data,temp,size * sizeof(int));  
    free(counts);  
    free(temp);  
  
    return 0;  
}  
  
int main()  
{  
    int a[] = {1,0,2,1,4,5,7,4};  
    int size = sizeof(a) / sizeof(a[o]);
    int max = a[0];
 
    for(int i = 0; i < size; ++i) // 1. find max in a[]
    {
        if(a[i] > max)
        {
            max = a[i];
        }
    }
    
    cnt_sort(a, len, max + 1); // 由于有0所以需要加1
 
    for(int i = 0; i < size; ++i)
    {
        cout<<a[i]<<endl;
    }
    
    return 0;
}

 

 

6.计数排序算法C++源代码

计数排序算法C++源代码
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
/**
* 算法君：一个专业的算法学习分享网站
* 算法君：专业分享--数据剖析--算法精解
* 算法君：http://www.suanfajun.com
*/
 
 
#include <iostream>
 
using namespace std;
 
void print(int a[], int sz) {
    for (int i = 0; i < sz;  i++ ) cout << a[i] << " ";
    cout << endl;
}
 
void CountingSort(int arr[], int sz) {
    int i, j, k;
    int idx = 0;
    int min, max;
 
    min = max = arr[0];
    for(i = 1; i < sz; i++) {
        min = (arr[i] < min) ? arr[i] : min;
        max = (arr[i] > max) ? arr[i] : max;
    }
 
    k = max - min + 1;
    /* creates k buckets */
    int *B = new int [k];
    for(i = 0; i < k; i++) B[i] = 0;
 
    for(i = 0; i < sz; i++) B[arr[i] - min]++;
    for(i = min; i <= max; i++)
        for(j = 0; j < B[i - min]; j++) arr[idx++] = i;
 
    print(arr,sz);
 
    delete [] B;
}
 
int main()
{
    int a[] = {5,9,3,9,10,9,2,4,13,10};
    const size_t sz = sizeof(a)/sizeof(a[0]);
    print(a,sz);
    cout << "----------------------\n" ;
    CountingSort(a, sz);
}

计数排序算法C++源代码
C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
/**
* 算法君：一个专业的算法学习分享网站
* 算法君：专业分享--数据剖析--算法精解
* 算法君：http://www.suanfajun.com
*/
 
 
#include <iostream>
#include <vector>
#include <time.h>
using namespace std;
#define  N 10   //排序数组大小
#define  K 100   //排序数组范围0～K
 
void CountSort(vector<int> &A)
{
     //找出待排序数组最大、最小值
     int min,max;
     min=max=A[0];
     for (int i=1;i<A.size();i++)
     {
         if (A[i]<min) min=A[i];
         else if (A[i]>max) max=A[i];        
     }
     //定义数组B存放排好的数
     vector<int> B(A.size());
     //定义数组C，大小为（max-min+1）,C[i]为A中值为i的个数
     vector<int> C(max-min+1);
     for (int i=0;i<max-min+1;i++)
                C[i]=0;//初始为0
     for(int i=0;i<A.size();i++)
                C[A[i]-min]++;//计数
     for (int i=1;i<max-min+1;i++)
                C[i]+=C[i-1];//累加
     for (int i=A.size()-1;i>=0;i--)
     {
         B[C[A[i]-min]-1]=A[i];//A中值倒序取出放到B中合适位置，并在C计数中减1
                                          //因数组下标从0开始，所以减1
         C[A[i]-min]--;
     }
     A.assign(B.begin(),B.end());//B赋给A
}
//打印数组
void print_element(vector<int> A)
{
     int len=A.size();
     for (int i=0;i<len;i++)
     {
         std::cout<<A[i]<<" ";
     }
     std::cout<<std::endl;
}
// 随机参数排序数组,产生数组范围0～k的整数
void Random(vector<int> &a,int n,int k)  
{  
     int i=0;  
     srand( (unsigned)time( NULL ) );  
     while(i<n)  
     {  
         a[i++]=rand()%k;  
     }  
}  
int main()
{
     vector<int > vec_int(N);
     Random(vec_int,N,K);
     cout<<"源数组： ";
     print_element(vec_int);
     CountSort(vec_int);
     cout<<"以排序数组： ";
     print_element(vec_int);
     system("PAUSE");
     return 0;
}

 

 

版权声明：本文著作权归原作者所有，欢迎分享本文，谢谢支持！
转载请注明：常用12大排序算法之十一：计数排序算法（原理与代码实现） | 算法君
分类：数据结构 标签：,

发表评论


表情